1°
a) Mediatriz
- La mediatriz de un triángulo es la mediatriz asociada a uno de sus lados, es decir, la recta perpendicular a dicho lado que pasa por el punto medio (o centro) de éste. La mediatriz de un segmento es una recta, lugar geométrico de los puntos que equidistan de los extremos de dicho segmento
b)Circuncentro
- El circuncentro de un triángulo es el punto donde se cortan las mediatrices de los lados. Dicho punto equidista de los vértices y, por lo tanto, es el centro de la circunferencia circunscrita al triángulo.
a)Circunferencia circunscrita
Un polígono que tiene una circunferencia circunscrita s
e llama polígono cíclico. Todos los polígonos simples regulares, todos los triángulos y todos los rectángulos son cíclicos. En todo polígono cíclico, el circuncentro se halla en el punto de intersección de las mediatrices de los lados del polígono.
e llama polígono cíclico. Todos los polígonos simples regulares, todos los triángulos y todos los rectángulos son cíclicos. En todo polígono cíclico, el circuncentro se halla en el punto de intersección de las mediatrices de los lados del polígono.
(https://es.wikipedia.org/wiki/Circunferencia_circunscrita)
2°
a)
Mediana
Las medianas de un triángulo (líneas rojas) se cortan en el baricentro del mismo. En geometría las medianas (en algunos países también llamadas transversales de gravedad) de un triángulo son, cada uno de los tres segmentos que unen cada vértice con el punto medio de su lado opuesto.
(https://es.wikipedia.org/wiki/Mediana_(geometría))
b)
Centro de gravedad: baricentro
El baricentro es el punto de corte de las tres medianas. Las medianas de un triángulo son las rectas que unen el punto medio de un lado del triángulo con el vértice opuesto. El baricentro se expresa con la letra G
(www.ditutor.com/geometria/baricentro.html)
3°
a)
Altura
La altura de un triángulo es el segmento perpendicular a un lado que va desde el vértice opuesto a este lado (o a su prolongación). También puede entenderse como la distancia de un lado al vértice opuesto.
(www.universoformulas.com/matematicas/geometria/altura-triangulo/)
b)
Ortocentro
El ortocentro de un triángulo es el punto de intersección de las tres alturas del triángulo (siendo una altura el segmento que parte de un vértice y es perpendicular al lado opuesto a dicho vértice)
(gaussianos.com/los-centros-del-triangulo-incentro-baricentro-circuncentro-y-ortocentro/)
4°
a)
Bisectriz
La bisectriz de un ángulo es la semirrecta que pasa por el vértice del ángulo y lo divide en dos partes iguales. Es el lugar geométrico de los puntos del plano que equidistan (están a la misma distancia) de las semirrectas de un ángulo.
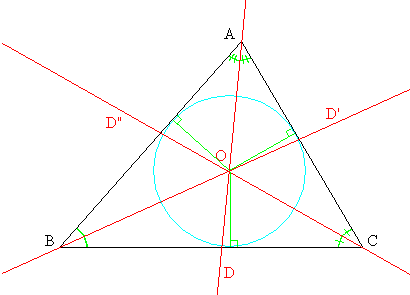
(https://es.wikipedia.org/wiki/Bisectriz)
Incentro
El Incentro de un triángulo (marcado con la letra I en el gráfico) es el punto en el que se cortan las tres bisectrices de sus ángulos internos. Equidista de los tres lados, y por lo tanto, es el centro de la circunferencia inscrita en el triángulo, tangente a sus tres lados.
(https://es.wikipedia.org/wiki/Incentro)
c)
Circunferencia Inscrita
En geometría, la Circunferencia inscrita o círculo inscrito de un triángulo es el círculo más grande contenido en el triángulo; toca (es tangente a) los tres lados. El centro de la circunferencia inscrita se llama incentro del triángulo.
5°
a)
Recta Euler
La recta de Euler de un triángulo es aquella recta en la que están situados el ortocentro, el circuncentro y el baricentro de un triángulo; además incluye al punto de Exeter y al centro de la circunferencia de los nueve puntos notables de un triángulo no equilátero.
(https://es.wikipedia.org/wiki/Recta_de_Euler)
No hay comentarios:
Publicar un comentario